В математике есть множество чисел с уникальными свойствами, которые могут удивить даже опытных специалистов. Удивительные числа — это не просто абстракции, а жемчужины числового мира, открывающие новые горизонты в понимании математических закономерностей. В этой статье мы рассмотрим, что такое удивительные числа, их необычные свойства и применение в науке и технике. Понимание этих чисел расширяет кругозор и развивает логическое мышление и аналитические способности.
Удивительные свойства простых чисел
Многие из нас, вероятно, замечали, что иногда удивляют не сложные вещи, а самые простые. Это правило также применимо к числовому миру.
Простыми числами называют натуральные числа, которые делятся только на единицу и на самих себя. Среди них можно встретить интересные пары, известные как числа-близнецы, которые отличаются друг от друга на 2. Например: 5 и 7; 11 и 13; 17 и 19. В пределах первых ста чисел можно найти всего 8 таких пар. По мере увеличения расстояния от нуля количество таких пар уменьшается. Интересно, что близнецы могут образовывать группы, создавая «четверки», такие как 11, 13, 17, 19. Однако, сколько таких групп можно образовать, пока остается загадкой.
В математике существует понятие, известное как «проблема Гольдбаха». Суть этой проблемы заключается в том, что еще в 1742 году Гольдбах, будучи членом Петербургской Академии наук, заметил, что любое целое число натурального ряда, превышающее пятерку, может быть представлено в виде суммы, состоящей максимум из трех простых чисел. Например: 34=31+3, 52=48+4 и так далее.
Ученый проверил множество чисел, и каждое из них оказалось суммой, состоящей из 2 или 3 слагаемых.
Российский математик Л. Эйлер пошел еще дальше, выдвинув гипотезу, что любое четное число натурального ряда, превышающее двойку, может быть представлено в виде суммы двух простых чисел. Например: 28=11+17=23+5; или 12=5+7; 64=59+5=41+23=47+17.
Удивительные числа представляют собой уникальные математические объекты, обладающие особыми свойствами и характеристиками. Эксперты в области математики отмечают, что такие числа часто вызывают интерес не только у ученых, но и у любителей чисел. Например, числа Фибоначчи, которые встречаются в природе, архитектуре и искусстве, демонстрируют гармонию и симметрию. Другим примером являются простые числа, которые играют ключевую роль в теории чисел и криптографии. Математики подчеркивают, что удивительные числа могут служить источником вдохновения для новых открытий и исследований. Их изучение помогает глубже понять структуру чисел и их взаимосвязи, что, в свою очередь, открывает новые горизонты в математике и смежных науках.

Открытия о составных числах
Не меньше вопросов и споров возникает при изучении составных чисел – величин, имеющих более двух делителей.
| Аспект | Описание | Примеры |
|---|---|---|
| Определение | Число, сумма всех делителей которого (включая само число) равна удвоенному значению этого числа. | 6 (1+2+3+6 = 12 = 26), 28 (1+2+4+7+14+28 = 56 = 228) |
| Другое название | Совершенные числа | |
| Связь с простыми числами Мерсенна | Все известные совершенные числа имеют вид $2^{p-1}(2^p-1)$, где $2^p-1$ является простым числом Мерсенна. | Для p=3, $2^{3-1}(2^3-1) = 2^2(2^3-1) = 4(7) = 28$ |
| Четность | Все известные совершенные числа являются четными. | 6, 28, 496, 8128 |
| Нечетные совершенные числа | Существование нечетных совершенных чисел до сих пор не доказано и не опровергнуто. | Гипотетическое нечетное совершенное число должно быть очень большим. |
| История | Изучались еще древнегреческими математиками, такими как Евклид. | Евклид описал формулу для четных совершенных чисел. |
| Количество | Известно лишь конечное число совершенных чисел, но предполагается, что их бесконечно много. | На 2023 год известно 51 совершенное число. |
Интересные факты
Вот несколько интересных фактов о удивительных числах:
-
Число Фибоначчи: Последовательность Фибоначчи начинается с 0 и 1, а каждое следующее число является суммой двух предыдущих. Эти числа встречаются в природе, например, в расположении листьев на стебле, в спиралях раковин и в числах цветков.
-
Число π (пи): Это удивительное число, представляющее собой отношение длины окружности к её диаметру, является иррациональным и трансцендентным. Оно имеет бесконечное количество знаков после запятой и не повторяется, что делает его объектом изучения и увлечения для математиков и любителей чисел.
-
Число e: Это основание натурального логарифма, примерно равное 2.71828, также является иррациональным и трансцендентным. Оно играет ключевую роль в математике, особенно в области анализа и теории вероятностей, а также в моделировании процессов роста и распада.
![Почему простые числа образуют спирали? [3Blue1Brown]](https://i.ytimg.com/vi/DxntHp7-wbg/maxresdefault.jpg)
Замечательные «смиты»
Эта категория чисел называется смитовыми, и она включает составные числа, сумма цифр которых в десятичной системе равна сумме цифр их простых множителей с учетом кратности. Таких чисел бесконечно много, и они удобно организованы в виде степеней. Чаще всего их можно встретить среди фигурных чисел: например, 22 – это пятиугольное число, 378 – треугольное, а 121 – квадратное.
Ярким примером смитового числа является равенство 2 × 101 = 202, где сумма цифр с обеих сторон знака равенства равна 4. Так, 2 + 0 + 2 = 4, и 2 + 1 + 0 + 1 = 4.
В мире смитовых чисел можно встретить множество интересных особенностей:
- Первые – это числа с повторяющимися цифрами (например, 1111, 666).
- Вторые – палиндромные числа, которые читаются одинаково в обе стороны, такие как 864468 и 3663.
- Третьи – это числа с привлекательными комбинациями цифр (например, 67067, 654).
Особенно интересными являются десятизначные смитовые числа, в которых каждая цифра встречается только один раз. Примеры таких чисел: 9 876 542 103 и 1 023 465 798.
Цикличность величины 142857
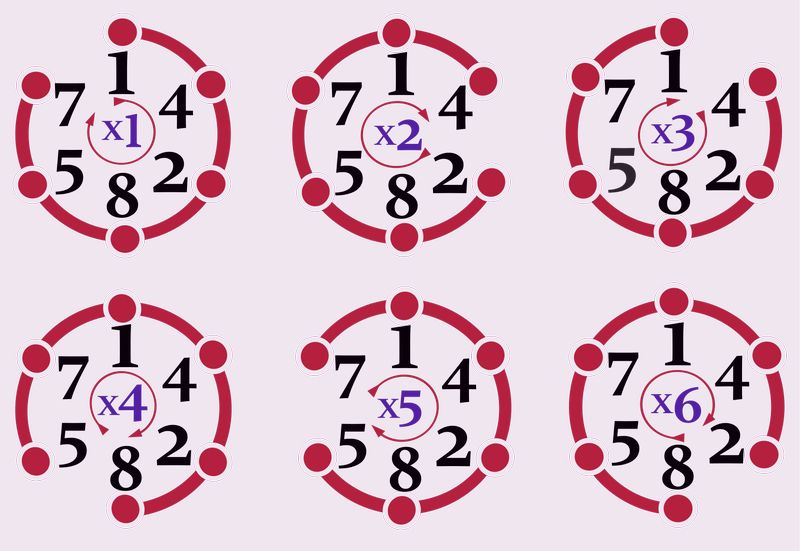
Одним из самых удивительных чисел по праву можно считать 142857. Оно необычно тем, что при умножении каждой из первых шести величин натурального ряда на него в результате будет получаться цилиндрический сдвиг этого шестизначного числа. В ответе каждый раз будут присутствовать одни и те же цифры, только они будут смещаться, двигаясь по типу ленты.
Для наглядности:
- 1 × 142857 = 142857
- 2 × 142857 = 285714
- 3 × 142857 = 428571
- 4 × 142857 = 571428
- 5 × 142857 = 714285
- 6 × 142857 = 857142
Секрет такой удивительной периодичности кроется в том, что 142857 выступает периодом преобразования простой дроби 1/7 в десятичную. Поэтому значения, расположенные после знака «=» являются периодами дробей: 1/7, 2/7, 3/7…

Число Шахерезады
Не менее увлекательно и «число Шехеризады». Оно является центральной темой в сборнике арабских сказок «Тысяча и одна ночь». Это число удивляет благодаря множеству уникальных характеристик. Рассмотрим лишь некоторые из них:
- Это наименьшее четырехзначное число в натуральном ряду, которое можно представить как сумму двух слагаемых, каждое из которых является натуральным числом, возведенным в куб: 1001=10•10•10+1•1•1=103+13;
- В его составе содержится 143 семерки. 7•143 =1001. Кроме того, один из множителей этого произведения «7» обладает магическими свойствами.
- Оно формируется из 91 «одиннадцатки»: 11•91=1001.
- Включает 77 «тринадцаток»: 77•13=1001. При этом оба множителя этого произведения наделены магическими свойствами: 13 – число, вызывающее страх у многих, а 77 – символ бесконечности в священных текстах.
1001 – это палиндром, то есть число, которое читается одинаково в обе стороны благодаря своей симметрии. Например:
Еще одно замечательное свойство 1001 заключается в том, что при умножении на него любой трехзначной величины результатом будет та же самая величина, записанная дважды. Например: 756х1001=756756. Зная эту особенность, любой желающий сможет легко умножать на 1001 любые трехзначные числа.
Золотое сечение
Что объединяет пальцы человеческой ладони и спирали улитки, древнеегипетские пирамиды и произведение «Мона Лиза»? Ответ кроется в удивительных числах, а точнее их последовательности, которые являются божественной мерой красоты.
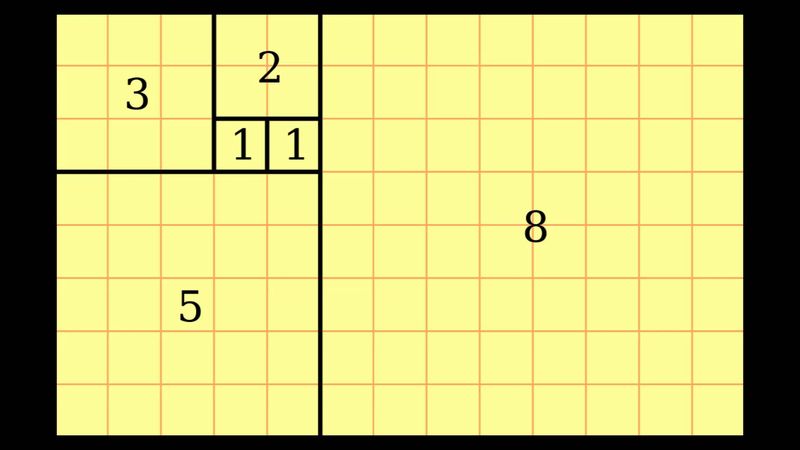
Последовательность, именуемая как ряд Фибоначчи, уникальна тем, что каждое «звено цепи» образуется из суммы двух предыдущих. Вот как выглядит эта цепочка: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
Составляющие ее величины имеют еще одну интересную особенность. Если разделить любую величину из «цепи» на предшествующую ей, в ответе всегда будет значение, максимально приближенное к иррациональному числу, десятичное представление которого всегда не периодично и бесконечно. Это 1.61803398875…
Это соответствие частей называется Золотое сечение. 1,6180339887 – величина, которая очерчивает совершенные универсальные пропорции в изобразительном искусстве и науке. Считается, что две величины находятся в Золотой пропорции, если их коэффициент к большей является точно таким же, как и соразмерность между большей и меньшей. Варианты таких соразмерностей:
- 2584/1597;
- 233/144;
- 1597/987;
- 987/610;
- 377/233;
- 610/377.
Формообразующий закон симметрии с удивительной настойчивостью проявляется в объектах, несущую эстетическую ценность у разных народов и эпох. Исходя из общепринятой пропорции, свои расчеты сегодня производят ученые.
Дизайнеры и модельеры берут за основу мерки с фигуры человека, которая построена по закону Золотой пропорции. Вот лишь некоторые соотношения 1:1.618, которые неизменно прослеживаются в теле любого человека. На голове это расстояние:
- от затылка до верхней линии бровей;
- от бровей до подбородка;
- от ноздрей до края верхней губы;
- от верхней губы до центра подбородка.
На туловище:
- от затылка до плеча;
- от затылка до пупка;
- от пупа до коленной чашечки;
- от колена до стопы;
- от запястья до кончиков пальцев 1:1.618;
Ведь многочисленные исследования подтверждают: если пропорции любых частей тела приближены к пропорции золотого сечения – получается идеальное телосложение, что выступает ключевым критерием красоты.
Математическая константа Пи
Самая известная математическая константа отражает отношение окружности к диаметру круга. Ее обозначение происходит от первых букв греческих слов, означающих «периметр» и «окружность».
Главная особенность этого удивительного числа заключается в том, что оно бесконечно и не имеет повторяющихся последовательностей. Первые 50 знаков после запятой выглядят следующим образом:
3,141592653589793238462643383279502884197169399375105
В 2011 году японский ученый с помощью мощного компьютера вычислил максимальное количество цифр числа Пи, которое составило 10 триллионов. В ходе работы он сделал интересное статистическое наблюдение. В первом миллионе знаков после запятой были зафиксированы следующие количества:
- «0» – 99959 раз;
- «1» – 99758 раз;
- «2» – 100026 раз;
- «3» – 100229 раз;
- «4» – 100230 раз;
- «5» – 100359 раз;
- «6» – 99548 раз;
- «7» – 99800 раз;
- «8» – 99985 раз;
- «9» – 100106 раз.
Число Пи находит применение в сферах, требующих высокой вычислительной мощности, таких как метеорология и глобальная социально-экономическая статистика. Ярким примером применения числа Пи является пирамида Хеопса в Каире, где соотношение высоты сооружения к периметру его основания также соответствует этому числу.
Распространенные числовые суеверия
Предубеждения, связанные с удивительными свойствами чисел – одни из самых распространенных и долгоживущих. У многих из нас есть свое любимое число, которое непременно приносит удачу. Все это отголоски представлений наших предков о мистической силе производящих счет величин.
Священное число 7
Число 7 занимает центральное место в различных религиях по всему миру. У христиан это 7 добродетелей, в исламе – 7 райских врат, а в буддизме – 7 сокровищ чакравартина.
Это божественное число олицетворяет гармонию и совершенство:
- Человек воспринимает информацию через 7 точек на голове (2 глаза, 2 уха, рот и 2 ноздри);
- Клетки нашего организма обновляются каждые 7 лет;
- Период беременности составляет 280 дней, что равно 40•7;
- Мы прекращаем расти в 21 год, что соответствует 7•3;
- Процесс высиживания птенцов и размножение млекопитающих также связано с числом 7;
- В природе можно выделить 7 основных металлов;
- Солнце в 49 раз больше нашей планеты, что также является 7•7.
Однако главная причина, по которой это число имеет особое значение для людей, заключается в том, что все живые существа живут по лунному циклу, состоящему из 4 фаз, каждая из которых длится 7 дней.
Исследования показывают, что 7 – это максимальное количество элементов, которые может удерживать в памяти человеческий мозг. Из 10 представленных объектов или произнесенных слов человек способен вспомнить только 7. Для эффективной работы творческой группы оптимальное количество участников также составляет 7. Если в переговорах участвует более 4 человек, группа начинает распадаться на подгруппы с общими интересами.
Число Зверя
666 – составное число Смита удивительно тем, что его можно записать в двух вариантах при возрастающем порядке, используя для этого 9 неповторяющихся цифр, и одним вариантом в убывающем:
- 123+456+78+9=666
- 1+2+3+4+567+89=666
- 9+87+6+543+21=666
К тому же эта величина выступает:
- Суммой своих же цифр и их значений, возведенных в третью степень: 6+6+6+63+63+63=666.
- Суммой и разностью первых величин натурального ряда, возведенных в шестую степень: 16−26+36=666.
Но для большинства людей эта величина известна под названием как «число Зверя». В Библии «7» упоминается как чистота и полноценность. Это 7 дней сотворения, 7 смертных грехов, 7 таинств. Шестерка – наоборот, нечто неполное и несовершенное, подобно Божему врагу.
Троекратность в 666 оказывает усиливающий негативный эффект, делая его символом крайней степени несовершенства. Обладает ли разрушительной силой эта величина доподлинно неизвестно. Но с десятки сотен фактов связанные с его негативным воздействием в истории человечества все же наберется.
Чертова дюжина
Существует широко распространенное мнение, что число 13 приносит несчастья. Это число имеет поклонников среди кабалистов, а в картах Таро оно ассоциируется со смертью. Корни этого суеверия уходят в религиозные верования, согласно которым 13-м ангелом считался будущий повелитель ада.
С математической точки зрения 13 является:
- нечетным двузначным числом, которое занимает 7-е место в последовательности Фибоначчи;
- наибольшим числом в примитивной пифагоровой тройке (5, 12, 13).
Людей, испытывающих страх перед числом 13, называют трискаидекафобами. Чтобы не вызывать у них беспокойства, многие европейские здания пронумерованы без этой цифры, а в некоторых высотках после 12-го этажа сразу идет 14-й. Также 13-й номер отсутствует в нумерации кают на кораблях, а в самолетах часто нет 13-го ряда.
В странах Азии число 13 воспринимается как обычное. Здесь больше опасаются числа четыре, так как оно символизирует смерть.
Несмотря на свою кажущуюся простоту, мир полон тайн и загадок. Однако разгадать их могут лишь самые любознательные умы.
Удивительные числа в природе и искусстве
Удивительные числа можно встретить не только в математике, но и в природе, искусстве и архитектуре. Эти числа часто обладают уникальными свойствами, которые делают их особенно интересными для изучения и наблюдения.
Одним из самых известных примеров удивительных чисел является число Фибоначчи. Эта последовательность начинается с 0 и 1, а каждое следующее число является суммой двух предыдущих. Числа Фибоначчи можно найти в природе, например, в расположении листьев на стебле, в спиралях раковин и даже в структуре соцветий некоторых растений. Эти числа также используются в искусстве, например, в композиции картин и архитектурных формах, где пропорции, основанные на числах Фибоначчи, создают гармонию и эстетическую привлекательность.
Другим примером является золотое сечение, которое приближенно равно 1.6180339887. Это число часто встречается в природе, например, в пропорциях человеческого тела, в формах животных и в структуре кристаллов. Золотое сечение также широко используется в искусстве, особенно в живописи и архитектуре, где оно помогает создать сбалансированные и гармоничные композиции. Многие известные художники, такие как Леонардо да Винчи и Микеланджело, использовали золотое сечение в своих произведениях.
В архитектуре удивительные числа также играют важную роль. Например, число Пи (π), равное примерно 3.14159, используется для расчета окружностей и является основой для многих архитектурных форм, таких как купола и арки. Пи встречается в различных конструкциях, от древнегреческих храмов до современных зданий, и его свойства помогают создавать устойчивые и эстетически привлекательные формы.
Кроме того, треугольник Паскаля и числа Каталана также являются примерами удивительных чисел, которые находят применение в различных областях, включая комбинаторику и теорию вероятностей. Эти числа помогают решать сложные задачи и находить закономерности в различных системах.
Таким образом, удивительные числа не только представляют собой интересные математические концепции, но и имеют глубокие связи с природой и искусством. Их изучение открывает новые горизонты для понимания окружающего мира и вдохновляет на создание уникальных произведений искусства и архитектуры.
Вопрос-ответ
Что такое интересные числа?
Странное число — натуральное число, которое является избыточным, но не является полусовершенным. Другими словами, сумма собственных делителей (делители, включая 1, но не включая себя) числа больше самого числа, но сложением подмножества делителей нельзя получить само число.
Что такое уникальные числа?
В теории чисел уникальное простое число — это определённый вид простых чисел. Простое число p ≠ 2, 5 называется уникальным, если не существует другого простого q, такого что длина периода разложения в десятичную дробь обратной величины 1⁄p равна длине периода 1⁄q.
Что такое необычное число?
Положительное составное целое число N называется необычным числом, если его G(N) ≥ max[G(N/p), G(aN)] для всех простых множителей p числа N и для всех кратных a ∗ N числа N.
Почему 28 идеальное число?
2-е совершенное число — 28 имеет следующие собственные делители: 1, 2, 4, 7, 14. Их сумма равна 28.
Советы
СОВЕТ №1
Изучите основные свойства удивительных чисел, такие как их уникальные математические характеристики и применение в различных областях науки. Это поможет вам лучше понять, почему они вызывают интерес у математиков и ученых.
СОВЕТ №2
Попробуйте самостоятельно находить удивительные числа, используя различные математические методы и алгоритмы. Это не только развивает аналитическое мышление, но и делает процесс обучения более увлекательным.
СОВЕТ №3
Обсуждайте удивительные числа с друзьями или в учебных группах. Совместное изучение и обмен идеями могут привести к новым открытиям и углублению понимания темы.
СОВЕТ №4
Ищите примеры удивительных чисел в реальной жизни, таких как в природе, искусстве или архитектуре. Это поможет вам увидеть, как математика взаимодействует с окружающим миром и делает его более интересным.